If you’ve ever studied network theory or graph theory, you might be familiar with the concept of graphs. Graphs are mathematical structures that represent a collection of objects and the relationships between them.
They are widely used in computer science, mathematics, and other fields to model complex systems and analyze data. However, in recent years, a new type of network has gained attention – the hypergraph network.
So, what is a hypergraph network? In simple terms, a hypergraph is an extension of a graph that allows edges to connect more than two vertices.
In a graph, an edge connects two vertices, whereas in a hypergraph, an edge can connect any number of vertices.
This may seem like a minor difference, but it has significant implications for how we model and analyze complex systems.
Hypergraphs vs. Graphs
To better understand the concept of hypergraph networks, let’s compare them to traditional graphs.
A graph is a collection of vertices (also known as nodes) connected by edges. The edges in a graph represent the relationships between vertices, which can be binary or non-binary. For example, in a social network graph, vertices could represent individuals, and edges could represent friendships between individuals.
A binary edge would represent a friendship between two individuals, whereas a non-binary edge could represent a group of friends.
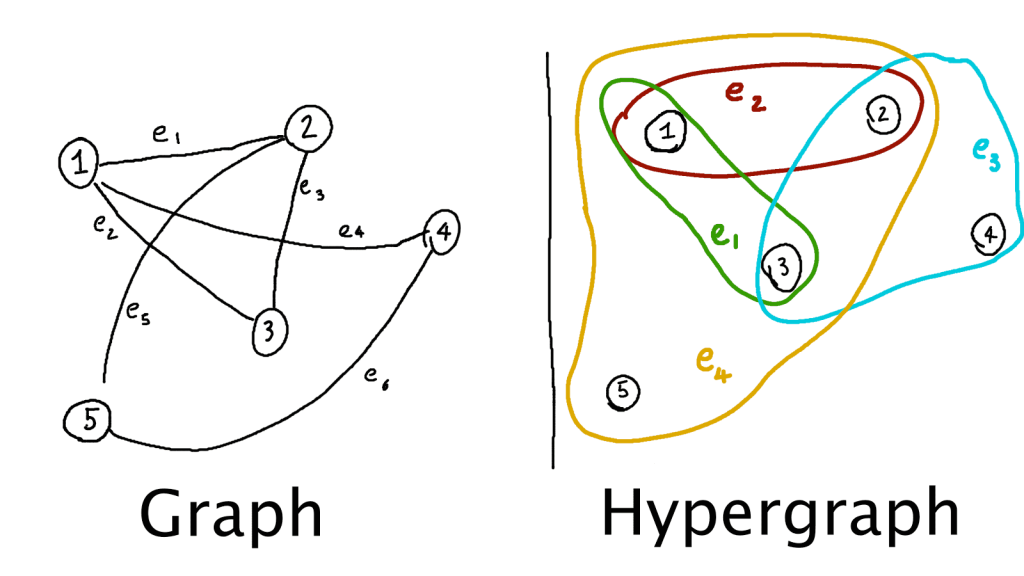
On the other hand, in a hypergraph network, we have hyperedges that can connect any number of vertices.
For example, in a protein interaction network, a hyperedge could represent a group of proteins that interact with each other.
In this case, the hyperedge could connect more than two proteins, which is not possible in a traditional graph.
Representation and Properties
In a hypergraph network, a hyperedge connects a set of vertices, which are referred to as hypernodes.
A hyperedge can contain any number of hypernodes, including a single hypernode. The number of hypernodes in a hyperedge is known as the hyperedge order.
For example, a hyperedge with two hypernodes is called a 2-hyperedge, and a hyperedge with three hypernodes is called a 3-hyperedge.
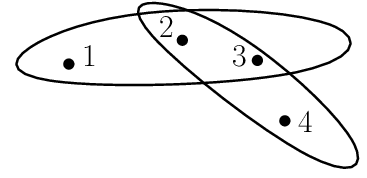
Hypergraphs also have some unique properties that distinguish them from graphs. One such property is the hyperdegree of a vertex, which is defined as the number of hyperedges that the vertex belongs to.
In a graph, the degree of a vertex is defined as the number of edges that the vertex is incident on.
The hyperdegree is a useful metric in hypergraph analysis as it allows us to identify important vertices in the network.
Another unique property of hypergraphs is the hyperpath and the hypercycle.
A hyperpath is a sequence of hyperedges where each successive hyperedge shares a hypernode with the previous one. A hypercycle is a hyperpath that starts and ends on the same hypernode.
Applications
Hypergraph networks have numerous applications across different domains.
In biology for example, in a protein interaction network, traditional graphs fail to capture the complex relationships between proteins. However, hypergraphs allow us to represent the interactions between proteins at a higher level of abstraction.
In social networks, hypergraphs can be used to model group interactions, social communities, and influence networks.
Hypergraphs are also used in transportation networks, recommendation systems, and data mining.
Hypergraphs are particularly useful in cases where traditional graph models are inadequate.
Algorithms and Techniques
Hypergraph networks require specialized algorithms and techniques for analysis due to their unique properties.
One such technique is hypergraph clustering, which groups vertices that belong to the same hyperedge. Hypergraph clustering can be used to identify communities or modules in the network.
Another technique is hypergraph partitioning, which divides the hypergraph into smaller subgraphs while minimizing the number of hyperedges that cross partition boundaries. This technique is commonly used in parallel computing to distribute workloads across multiple processors.
Hypergraph matching is another important algorithm for hypergraph analysis. It involves finding a one-to-one mapping between hyperedges in two hypergraphs that maximizes the number of matched hyperedges. Hypergraph matching is useful in applications such as pattern recognition and image analysis.
Is there a relation between Hypergraph and Hedera Hashgraph?
Despite the similarity in names, Hypergraph and Hedera Hashgraph are not directly related.
Hypergraph is a mathematical concept that extends the traditional graph model to allow for hyperedges, which can connect more than two vertices. Hypergraphs are used for modeling complex systems and analyzing data in various domains.
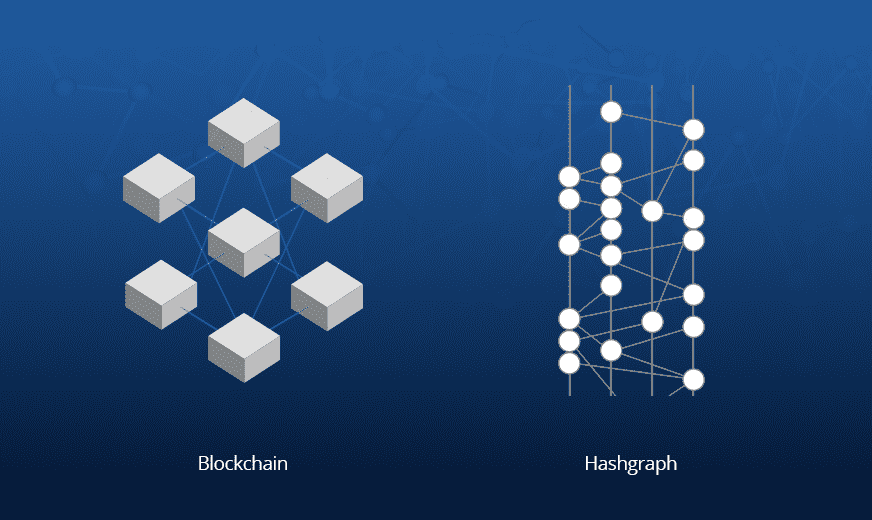
On the other hand, Hedera Hashgraph is a distributed ledger technology that uses a consensus algorithm to achieve fast and secure transactions. Hedera Hashgraph is designed to be a fast, fair, and secure platform for decentralized applications (DApps) and enterprises.
While both Hypergraph and Hedera Hashgraph involve the concept of graphs, they are fundamentally different in their applications and uses.
It’s worth noting that although Hypergraph and Hedera Hashgraph are not directly related, there may be potential applications of hypergraphs in decentralized systems like Hedera Hashgraph.
As the field of hypergraph analysis continues to evolve, it’s possible that new techniques and algorithms will be developed that can be applied to various domains, including distributed ledger technologies.
Conclusion
- The bottom line is, hypergraph networks are an extension of traditional graphs that allow edges to connect more than two vertices.
- Hypergraphs have unique properties that make them useful for modeling complex systems and analyzing data.
- They have applications in a variety of domains, including biology, social networks, transportation, and data mining. Hypergraphs require specialized algorithms and techniques for analysis due to their unique properties.
- Hypergraph clustering, hypergraph partitioning, and hypergraph matching are some of the important techniques used for hypergraph analysis.
If you’re interested in learning more about hypergraphs and their applications, there are many resources available online.
Some popular hypergraph libraries include NetworkX and HyperNetX. These libraries provide tools for creating, manipulating, and analyzing hypergraph networks.
With the increasing popularity of hypergraph networks, we can expect to see more research and development in this area in the years to come.
Like what you’ve read? Check our Glossary page for more educational content.
Read Also
Previous Articles:
- Dragonfly Capital invests $10M in Bitget to drive crypto adoption
- Allbridge Reclaims Majority of Stolen Funds Through White Hat Bounty Offer
- South Korean Prosecutors Seize $160M in Assets Linked to Terraform Labs Collapse
- What Is The CryptoNote Protocol Monero Is Using?
- Flashbots Loses Around $20M in Innovative Cyber Attack: Insider Information Exploited by Hacker

